23. Rediseny del rall experimentat de 8 puntes i 3-1 increments, Teles de 50 i 60 malles

 0. Introducció



1. Nomenclatura i variables




Les variables a tindre en compte són:

y: Altura per on tallem la tela. 

ya: Altura on tallem el triangle

yb: Altura on tallem el trapeci. Si la tela es curta ya = yb = y

xi: Nombre de malles que queden en el triangle interior que tallem

x1: Nobre de malles que deixem a la part de dalt del trapezi abans d'unir amb el triangle interior que tallem

x2: Nombre de malles de la part de baix del trapezi

𝚫x: Serà la diferència entre x2 i x1 (i siga x2-x1)




2. Formes d'empalmar les puntes 


Forma 1 (y=4n)


Fig.1

Ací temin si aprofitem tota la tela posible:

y = 2 (xi +1) -> xi = (y/2) - 1

y= 2 (𝚫x -1) -> 𝚫x = (y/2) + 1

x1= xi - 1 -> x1 = (y/2) - 2

x2= x1 + 𝚫x = y - 1

Pero si hi ha certa independència del triangle i trapeci, anamenant ya a l'altura del triangle i yb a la del trapezi, sempre que ya i yb siguen del tipus 4 n 

ya = 2 (xi +1) -> xi = (ya/2) - 1

yb= 2 (𝚫x -1) -> 𝚫x = (yb/2) + 1

x1= xi - 1 -> x1 = (ya/2) - 2

x2= x1 + 𝚫x = (ya/2) + (yb/2) -1



Forma 2 (y=4n+1)


Fig.2

Análogament:

y = 2 (xi + 2.5) -> xi = (y/2) - 2.5

y= 2(𝚫x +0.5) -> 𝚫x = (y/2) -0.5

x1 = xi +3 = (y/2) + 0.5

x2= x1 + 𝚫x = y

I amb independència:

ya = 2 (xi + 2.5) -> xi = (ya/2) - 2.5

yb= 2(𝚫x +0.5) -> 𝚫x = (yb/2) -0.5

x1 = xi +3 = (ya/2) + 0.5

x2= x1 + 𝚫x = (ya/2) + (yb/2)


Forma 3 (y=4n+2)


Fig.3

Igualment:

y = 2 (xi +2) -> xi = (y/2) -2

y= 2 𝚫x -> 𝚫x = y/2

x1 = xi +1 = (y/2) - 1

x2= x1 + 𝚫x = y - 1

 amb independència:

ya = 2 (xi +2) -> xi = (ya/2) -2

yb= 2 𝚫x -> 𝚫x = yb/2

x1 = xi +1 = (ya/2) - 1

x2= x1 + 𝚫x = (ya/2) + (yb/2) - 1



Forma 4 (y=4n+3)

Fig.4

Finalment:

y = 2 (xi +1.5) -> xi = (y/2) - 1.5

y= 2 (𝚫x -0.5) -> 𝚫x = y/2 + 0.5

x1 = xi +1 = (y/2) - 0.5

x2= x1 + 𝚫x = y 

I amb independència de le altures:

ya = 2 (xi +1.5) -> xi = (ya/2) - 1.5

yb= 2 (𝚫x -0.5) -> 𝚫x = yb/2 + 0.5

x1 = xi +1 = (ya/2) - 0.5

x2= x1 + 𝚫x = (ya/2) + (yb/2)


Per tant per motius de simplicitat sembla millor buscar els patrons:

y = 4 n

y = 4 n + 2

3. Pèrdua de malles del triangle interior

Per a que coincidisca amb el càlcul del rall suposem que es talla la part superior del rall s'aplica el format 
y= 4n +1



Amb la qual cosa el nombre de malles x0 ve donada per la variable y que és el nombre de passades per onhm de tallar la part superior del triangle

y= 2( x0 + 1.5)

Però x0 sols pot valdre valors imparells ( 1, 3, 5, 7, 9, 11, 13, 15, 17 ...)

Y alguns valors són

 y(pèrdua)   x0   Nombre malles superiors (8 * x0)
 21   9  72
 25  11  88
 29  13  104
 33  15  120
 37  17  136


4. Passades per a tirants + bos

Segons la longitud dels tirants i del bos podem gastar entre 80 i 88 cm.

Suposant una longitud de costat de 2.5 cm ens queden entre 32 i 35 passades


5. Suposit 1 : Tela de 50 malles i 2.5 cm de costat

Ací hem d'aprofitar la tela al màxim, per tant tot el triangle que tallem s'ha d'aprofitar

En este cas la tela té 101 passades (2*50 males + 1 afegida)

Vegem les possibilitats que tenim

 A=
pas (tirant+bos)  		  (y) B=
altura a tallar
= (101-A) 		  Tipo  xi   x1  𝚫x   x2   Observacions 
 32  69  4n + 1               Descartat per ser 4n +1
 33  68  4n    33   32   35   67    Elecció !!!
 34  67  4n +3
            Descartat per se 4n + 3
 35  66  4n +2  31    32   33  65    Descartat per minimitzar l'altura

Vegem com queda a l'afegir  el triangle tenint en compte que y = 68 

 yperd
(pèrdua) 		  x0   Nombre
malles superiors
=(8 * x0)		 yresto=
 (y-yper)		 altura neta=
 y +yresto		 Observacions per a:
 tirant = 25 cm,
longitud nuc = 1 mm
OJO: Ixen 89,32 ploms !!!!
 21   9  72   47   115  R obert= 2,59 m 
 Plom+brag=18,2 cm
 L corda ploms= 16,27 m 
Angles (malla, tirant) 79 º i 94º
 25  11  88   43   111  R obert= 2,54 m 
 Plom+brag=17,9 cm
 L corda ploms= 16,01 m 
Angles (malla, tirant) 77 º i 92º
 29  13  104   39   107  R obert= 2,50 m 
 Plom+brag=17,6 cm
 L corda ploms= 15,72 m 
Angles (malla, tirant) 75 º i 90º
ELECCIÓ !!!
Ja que fa por de fer coca quan el nombre de malles superiors amb fil trençat es inferior a 90
 33  15  120   35   103  R obert= 2,45 m 
 Plom+brag=17,2 cm
 L corda ploms= 15,40 m 
Angles (malla, tirant) 74 º i 87º
 37  17  136   31   99  R obert= 2,39 m 
 Plom+brag=16,8 cm
 L corda ploms= 15,04 m 
Angles (malla, tirant) 72 º i 85º 


Però el nombre de ploms no ix parel sinó decimal, per tant hauriem d'aconseguir 90 ploms que corresponen a 540 malles i ara en tenim 536 (8 * 67)

Per a concloure es tallarà la tela així:

Cal observar que a l'últim pic de la corona hem afegit 4 malles per a que al final sume 540 malles i s'arreglen be les malles per els 90 ploms i tirants.






Això comporta que l'última peça B que està partida en 2 parts requerisca afegir estes 4 passades laterals d'unió dels semitriangles.


Anem a mostrar com quedarien els pedaços i afegits


.


6. Suposit 2 : Tela de 60 malles i 2.5 cm de costat

Ací ja ens sobra algo de tela ja que si intentem aprofitat tota la tela ens queda un rall massa gran i difícil de manejar

En este cas la tela té 121 passades (2*60 males + 1 afegida)

Per aconseguir un radi obert d'al voltant de 3 metres cal tenir almenys 135 passades incrementant

Ara podem emprar 35 passades per als tirant + bos 

Vegem les taules anteriors com queden, tenint en compte que hi ha independència d'altures, per tant sols poden calcular ara 𝚫x que és l'única que depén de yb


 A=pas (tirant+bos)    (yb) B=
altura a tallar
= (121-A) 		  Tipo  𝚫x   Observacions 
 32  89  4n + 1      Descartat per ser 4n +1
 33  88  4n    
 34  87  4n +3
  Descartat per se 4n + 3
 35  86  4n + 2  43   Podem elegir un poc més de
 bos  ja que ens sobra tela

Per a obtenir un radi obert de 3 m hem d'afegir al voltant de nafig = 49 passades (135 = 86 +49 ) pero hem de tindre en compte que:

  ya = yperd +  nafig siga de la forma 4 n +2 

Però per a no anar afegint malles a l'última corona, podem jugar amb les malles inicials (que com es més rígida la tela por tenir-ne menys), i el nombre de passades a afegir

Vegem com queda a l'afegir  el triangle tenint en compte que yb = 86

***********************************************************************

 yperd
(pèr
dua) 		  x0   Núm
malles
dalt
=8 * x0		 y
resto=
 y-yper		 ymax

 nafig

 ya=
y +
yper

 xi x1 x2 ytot
=
yb+
nafig		 Radi
obert		 Ploms
 21   9  72   65  151  45 
 49 
 53 		  66
 70
 74 		  31
 33
 35 		  32
 34
 36 		  75
 77
 79 		  131
 135
 139  		  2,90
 2,98
 3,05		  100
 102,66
 103,33
 25  11  88   61   147  45 
 49 
 53 		  70
 74
 78 		  33
 35
 37 		  34
 36
 38 		  77
 79
 81 		  131
 135
 139 		  2,94
 3,02 
 3,10		  102,66
 103,33
 108
 29  13  104   57   143  45 
 49 
 53 		  74
 78
 82 		  35
 37
 39 		  36
 38
 40		  79
 81
 83 		  131
 135
 139 		  2,98
 3,05
 3,13 
 103,33
 108
 110,66
 33  15  120   53   139  45 
 49 
 53 		  78
 82 
 84 		  37
 39 
 41 		  38
 40
 42 		  81
 83
 85 		  131
 135
 139  		  3,01
 3,09
 3,17		  108
 110,66
 113,33
 37  17  136   49   135  45 
 49 
 53 		  82 
 84 
 86 		  39 
 41 
 43 		  40
 42
 44 		  83
 85
 87 		  131
 135
 139  		  3,04
 3,12
 3,20 		  110,66 
 113,33
 116 

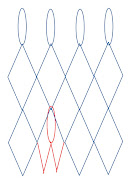
Y el tall a fer es veu en la figura:


I els càculs:










Comentaris

Publica un comentari a l'entrada

Entrades populars d'aquest blog

8. Encontre APARCOVA del 19/07/2025

Imatge
Tot i que el dia per a pescar era molt bo ja que feia ponent i la mar estava relativament tranquila, la zona, al estar lluny de les goles, no es veia peix, sols alguna mola de llisses de 10 cm que escapaven del rall. 1. Els preparatius S'ha previst ombratges per a combatre el calor ja que s'estava quasi a 40º.  . .. . . 2. La intendència Calia fer també ombratges per a la intendència, però com estaven darrere del muntanyar, de segur que hauran patit molta calor 3. Els mestres ensenyen l'art El gran Albert d'Almassora ens ensenya com preparar i llançar el rall de cercolet Juan el Mariner també conegut per Juan el Llarg (per la seua altura) també ens ensenya com arreglar i llançar el rall. 4. Per a tirar el rall sols cal un rall, mar i ganes Enric el president de l'Associació de Ralladors de Sueca, també ha fet acte de presència.  Enric ha aconseguit el somni d'un neòfit argentí que volia un rall valencià. El gran Javi Pachés a la dreta amb la càmera al cap, l...
Més informació

7. Encontre de ralladors al Mareny de Barraquetes el 12 de Juliol de 2025

Imatge
1. Primer que res a pescar! El dia es no semblava massa bo i sols han acudit a pescar uns pocs, la pesca és un aspecte simbòlic de la quedada. Allò que realment importava era esmorçar i intercanviar opinions. Durant la pesca, el nostre company "Fabat" ens ha mostrat el seu domini del rall, capturant, extranyament un nombre considerables de llisses, crancs i una morruda. I eixa ha sigut una de les anècdotes del dia; ha preguntat " Qui deia que no es pescaven morrudes al mes de juliol? " I jo tímidament he alçat la ma. Una rialla se li ha escapat al "Fabat" En esta foto es veu el "Fabat" amb una llissa dins del rall. Contingut d'un dels cabassos Altre cabàs El senyor president també ha fet alguna captura 😂I com es normal en este país, uns pocs treballen(millor dit: pesquen)  i els altres ens dediquem a mirar .... i ahí va la prova! Juan Vicente i el germà també s'han animat a pescar. 2. Ara toca posar-se el dia sobre la pesca Abans d'e...
Més informació

1. Calcular el radi d'un rall obert. Cal anar a l'entrada 14 que és més general

Imatge
 Per a calcular el radi d'un rall obert S'ha de saber els següents paràmetres: Per a calcular visita Càlcul radi del rall i amplaria del plom i braguerot sabent el nombre de punts inicial i final i longituds del tirant i del bos Longitud mitja malla en cm Longitud del costat del rombe de la malla Nombre de triangles En rall tradicional es el nombre d'afegits cada 3 passades Cada quantes passades afegim En rall tradicional cada quantes passades afegim Nombre de passades després de l'últim afegit i començament del tirant En rall tradicional Nombre de passades després de l'últim afegit i començament del tirant sense comptar l'afegit Nombre de punts primera passada El nombre de punts per passada al començar Nombre ...
Més informació